Berechnung der Umlaufdaten
Diese Seite befindet sich noch im Aufbau.

Quelle: Werren
Gravitationskonstante: G = 6,6741E-11 m³ / (kg * s2)
siderische Jaheslänge: Ts = 365,2563604167 d
Kreiszahl: pi = 3,14159265358979
Beide Objekte umlaufen in Ellypsenbahnen den gemeinsamen Schwerpunkt, der im jeweiligen Perihel- Brennpunkt liegt.
Die Schwerpunktabstände verhalten sich umgekehrt proportional zu den Massen:
Masse1-Gesamtschwerpunktabstand: s1 = r * m2 / (m1 + m2 )
Masse2-Gesamtschwerpunktabstand: s2 = r * m1 / (m1 + m2 )
Stabile Umlaufbahnen stehen im Gleichgewicht von Fliehkraft und Anziehungskraft:
FZ = FG
G * m1 * m2 / r2 = m1 * v12 / s
Orbitalgeschwindigkeiten:
Orbitlalgeschwindigkeit1: v1= Wurzel ( G * m1 * m2 * s1 / ( m1 * r2 ))
Orbitalgeschwindigkeit2: v2= Wurzel ( G * m1 * m2 * s2 / ( m2 * r2 ))
v1 = Wurzel ( G * m2 * s1 / r2 )
v2 = Wurzel ( G * m1 * s2 / r2 )
Bahnumfang:
Bahnumfang1: U1 = s1 * 2 pi
Bahnumfang1: U2 = s2 * 2 pi
Umlaufdauer:
T = U2 / v2
Beispielrechnung für die Erdbahn:
Quelle: Werren
Quelle: Werren
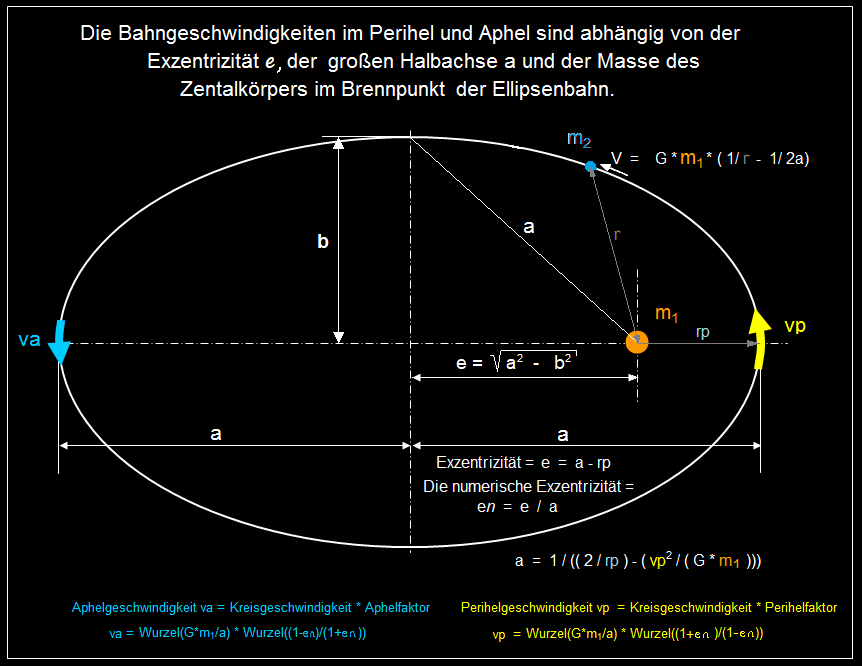
In Netz herrscht zwischen linearer und numerischer Exzentrizität Verwirrung über die Formelzeichen. Darum wird hier für die numerische Exzentrizität der Index n zu e verwendet.
Die lineare Exzentrizität e ist die real messbare Entfernung eines Brennpunkts bis zum Mittelpunkt der Ellipse.
Die numerische Exzentrizität en ist eine dimensionslose Verhältniszahl,
die das Verhältnis der linearen Exzentrizität zur großen Halbachse darstellt. Sie errechnet sich aus e / a.
Quelle: Werren

Quelle: Werren