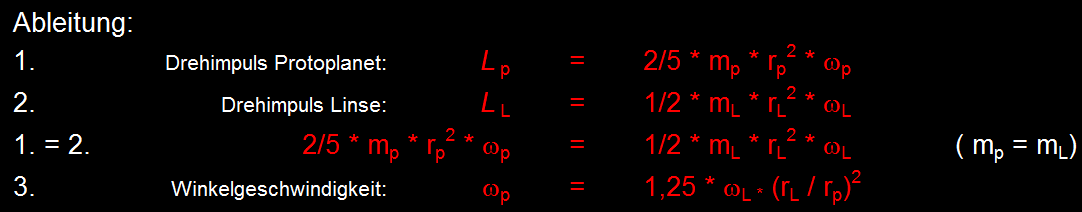Berechnung der Planeten- Eigendrehung nach Drehimpuls
Drehimpulsmethode
Um die Planetendrehzahlen zu ermitteln, müssen zunächst die Größen der Linsen berechnet werden.
Linsenradien:
Die Linsenradien lassen sich durch Gleichsetzen der Gravitationsfeldstärken FP und FL des Umlaufradius um die Protosonne mit dem der Grenzschicht ausrechnen.
Daraus ergibt sich:
Linsenradius = Umlaufbahnradius * Wurzel aus (Linsenmasse / Sonnenmasse)
Ermittlung der Planetendrehzahl
über die Winkelgeschwindigkeit:
Eine überschlägige Ermittlung der Planetendrehzahlen aus den Daten der Linsen und Protoplaneten ist nicht sehr aufwändig:
Dazu müssen nur die Drehimpulse der Linsen und der Protoplaneten gleichgesetzt werden.
Der Drehimpuls eines Protoplaneten LP ist:
0,4 * der Masse mP * Protoplanetenradius zum Quadrat rL2 * Winkelgeschwindigkeit wP.
Der Drehimpuls der Linse LL ist:
0,5 * der Masse mL * Linsenradius rL * Winkelgeschwindigkeit wL.
Die Massen mL und mP sind gleich.
Die unterschiedlichen Faktoren 0,4 und 0,5 beziehen sich auf die Trägheitsmomente von Kugel und Scheibe.
Nach Gleichsetzung und Auflösung nach Winkelgeschwindigkeit des Protoplaneten wP ergibt sich folgende Formel:
wP = wL * 1,25 * (rL / rP)2.
Leider sind die Verhältnisse komplizierter, denn wenn die Linse zum Protoplaneten kontrahiert, sedimentieren die Bestandteile je nach Dichte. Dadurch konzentriert sich auch zum Zentrum hin ein überproportionales Trägheitsmoment. Eine ausführlichere Rechnung zeigt deshalb von der Überschlagsrechnung abweichende Ergebnisse.