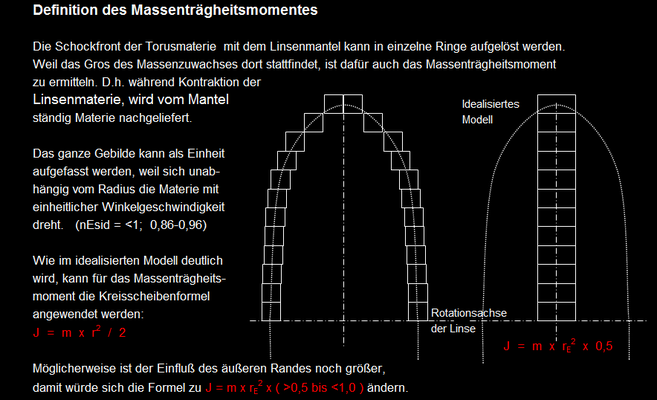
Planetendrehzahlberechnung nach Rotationsenergie
Die Rechnung basiert auf einfachen grundlegenden Formeln der Dynamik und Himmelsmechanik.
Eine akribisch genaue Rechnung, bei teils geschätzten Ausgangsdaten wäre unsinnig.
Der Tabelle ist eine ausführliche Erläuterung beigefügt.
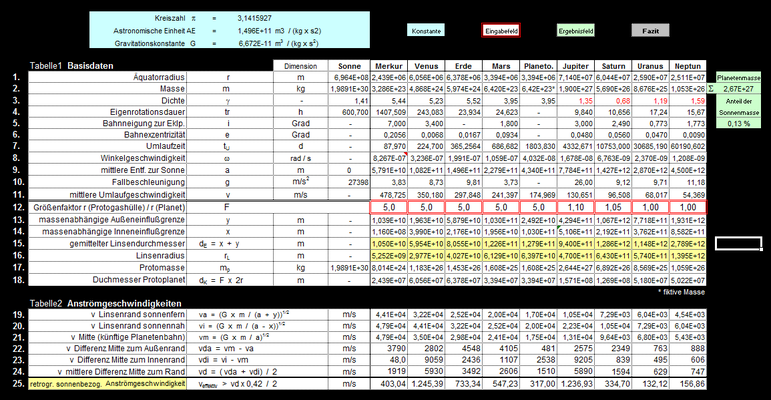
Für jeden Protoplaneten werden nur zwei Eingaben gefordert:
1. Der Größenfaktor, also das Verhältnis von Protoplanetendurchmesser zum aktuellen Durchmesser
2. Die mittlere Dichte der Protoplaneten- Gashülle und der Kerndichte der Gasplaneten
Die Planeten werden rechnerisch in den Protozustand versetzt: Dazu ist die Eingabe des Größenfaktors erforderlich. Bei Jupiter und Saturn gehe ich von einer Hülle aus,
die aufgrund der Zusammensetzung, seit der Protozeit nur einen geringen prozentualen Anteil verloren hat. Der Größenfaktor wird bei den beiden Gasplaneten mit einem Faktor von 1,1 und 1,05 angenommen. (Darüber hinaus gab es in den Gashüllen sicher auch noch chemische Reaktionen mit Vulkangasen) Es ist anzunehmen, dass die Atmosphären der äußersten Planeten Uranus und Neptun seit der Protozeit unverändert geblieben sind.
Die inneren Planeten werden ebenfalls mit einer Gashülle berücksichtigt.
Ihr Größenfaktor ist sehr viel schwieriger abzuschätzen, und damit zugegebenermaßen ein Schwachpunkt der Rechnung. Er sollte sich danach richten, welches Größenverhältnis zwischen festem Kern und Gashülle die Planetenforschung bei den Gasplaneten für realistisch hält. Meine geschätzten Eingaben ergeben in Durchmesser und Dichte,
ähnliche Verhältnisse wie bei Uranus oder Neptun.
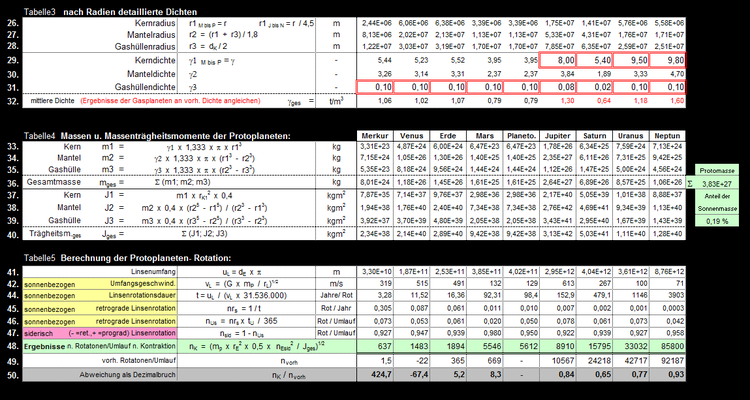
Um die Massenträgheitsmomente abzuschätzen, werden die Protoplaneten in 3 Schichten (Kern, Mantel und Hülle) mit unterschiedlicher Dichte unterteilt. (Kern und Mantel sind hier nicht geologische, sondern bildhafte Begriffe). Rechnerisch bilden die inneren Planeten die Kerne der Protoplaneten Merkur bis Mars. Dazu werden die aktuellen Daten aus Tabelle 1 übernommen. Die Hüllendichten sind so zu variieren, dass bei den inneren Planeten daraus ähnliche Gesamtdichten, wie bei den Gasplaneten resultieren.
Neben den Hüllendichten der Gasplaneten sind auch deren Kerndichten abzuschätzen.
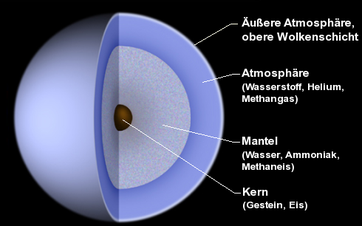
Vermuteter Schichtaufbau des Uranus. Quelle: FrancescoA
Die 3-Stufenschichtung ist der vereinfachten Rechnungsweise geschuldet.
Die Formel unter Punkt 48 berücksichtigt nicht, dass die Konzentration der schwersten Elemente im Planetenzentrum das Gesamtträgheitsmoment vermindert.
Das wird allerdings durch den Umstand wieder ausgeglichen, dass etwa 10%* (siehe Kapitel „Planetenembryos“) der Linsenmasse am Wechselwirkungseffekt nicht teilnehmen. Insgesamt darf man sich den Entwicklungsablauf nicht streng schematisch vorstellen, sondern eher so, dass alle Vorgänge kontinuierlich ineinander greifen.
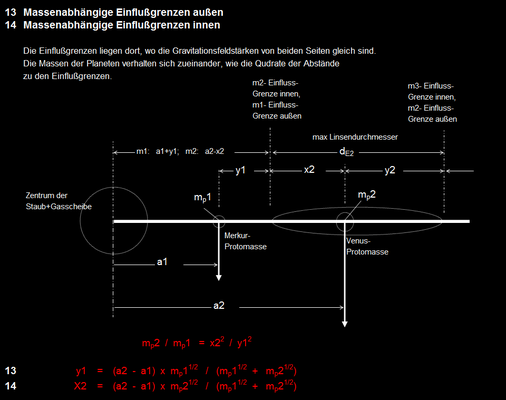
Die Einflussgrenzen werden aus den Massen der Protoplaneten errechnet.
Für Merkur liegt die innere Grenze auf dem Neutralpunkt zwischen Sonne und Merkur.
Weil für Neptun keine äußere Einflussgrenze existiert, wird sie aus den Durchschnittsverhältniszahlen der anderen Planeten errechnet.
Auf der Durchschnittsbahn der Planetoiden wurde ein fiktiver Planet von Marsgröße eingerechnet, um die äußere Einflussgrenze für Mars zu ermitteln.
Als Ergebnis werden die theoretischen Rotationszahlen je Sonnenumlauf ausgewiesen.
Im Vergleich der Planeten wird deutlich: Der Anteil der retrograden Komponente bleibt trotz der Unterschiede in Umlaufzeiten und Planetenradien fast gleich.
Bei den äußeren Planeten wird die geringere prograde Eigenrotation je Zeiteinheit,
bei der Kontraktion durch den stärkeren Wechselwirkungseffekt so kompensiert,
dass mit Ausnahme von Merkur und Venus, die Tageslängen aller Planeten in ähnlicher Größenordnung liegen.
Quelle: Werren
Erklärung der Rechenschritte:
oder zurück nach: